2 * n 타일링

1. 문제 설명

문제 설명 가로 길이가 2이고 세로의 길이가 1인 직사각형모양의 타일이 있습니다. 이 직사각형 타일을 이용하여 세로의 길이가 2이고 가로의 길이가 n인 바닥을 가득 채우려고 합니다. 타일을 채울 때는 다음과 같이 2가지 방법이 있습니다.

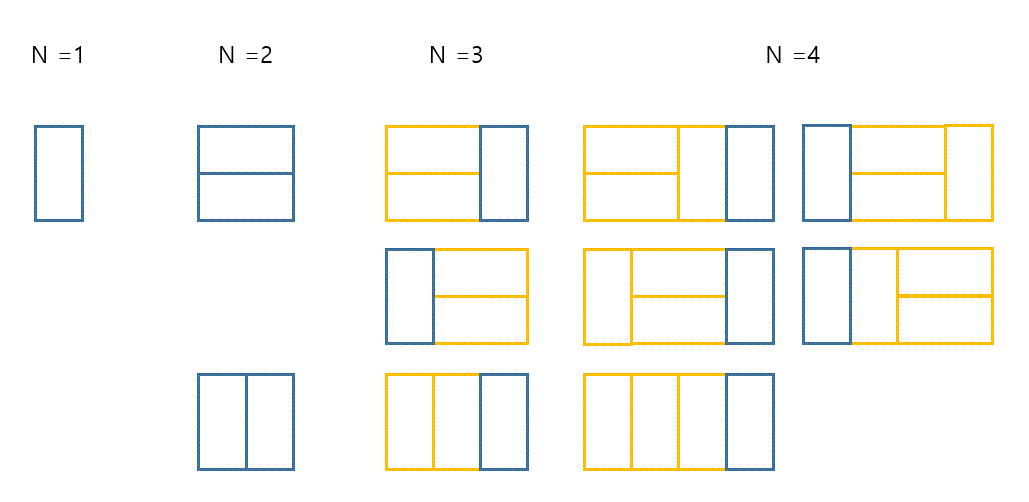
타일을 가로로 배치 하는 경우 타일을 세로로 배치 하는 경우 예를들어서 n이 7인 직사각형은 다음과 같이 채울 수 있습니다.

직사각형의 가로의 길이 n이 매개변수로 주어질 때, 이 직사각형을 채우는 방법의 수를 return 하는 solution 함수를 완성해주세요.

제한사항 가로의 길이 n은 60,000이하의 자연수 입니다. 경우의 수가 많아 질 수 있으므로, 경우의 수를 1,000,000,007으로 나눈 나머지를 return해주세요.

2. 해결 Point

이 문제의 핵심은 해당 문제가 피보나치 수열을 인 점을 알 수 있어야 한다.

우선 n = 1 인 경우 가능한 경우의 수는 무조건 1이다.

그리고 n = 2 인 경우 2개의 직사각형을 가로와 세로로 각각 배치해 총 2개의 방법이 있다.

이후 사각형의 경우의 수는 다음과 같이 생각하면 이 문제가 피보나치 문제인 것을 알 수 있다.

3. 이론

• DP (dynamic programming)

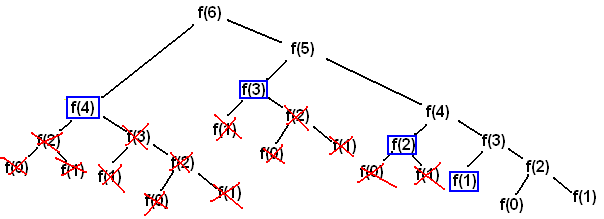
피보나치 함수를 푸는 가장 쉬운 방법은 재귀 함수를 이용한 방법 일 것이다.

f(n) = f(n-1) + f(n-2)

문제는 재귀 함수 방식을 이용하게 되면 n 부터 1까지 함수를 매번 호출하게 되기 때문에 컴퓨터 자원을 효율적으로 사용하지 못하게 된다.

그렇기 때문에 데이터를 함수에 저장해 해결하는 DP를 이용한다면 조금 더 효율적으로 피보나치 문제를 풀 수 있다.

4. Source Code

class Solution {

  public int[] array;

  public int solution(int n) {
    long answer = 0;
    array = new int[n+1];

    answer = fib(n);

    return (int) answer;
  }

  public long fib(int n){
    array[0] = 1;
    array[1] = 1;

    for(int i=2; i<=n; i++){
      array[i] = (array[i-1]+array[i-2]) % 1000000007;
    }
    return array[n];
  }
}